If you hear about elections, what do you think of? Probably human beings putting a small piece of paper into a ballot box in order to elect other human beings. But in reality, the scope of voting is much broader. Increasingly, the field of artificial intelligence (AI) allows the development of autonomous software agents that are able to make decisions on their own. And, like human beings, they may sometimes need to make decisions in community.
Intelligent agents voting on their own
For example, imagine robots from several companies working in the same warehouse. One of them finds an unidentified object acting as an obstacle in a common area. Several options are then possible: temporarily store it in various locations, put it in the dumpster, etc. A collective decision must then be made.
In the case of semi-autonomous vehicles platooning, they may choose their common speed and even possibly their route. But each vehicle, which may belong to different companies (or to the same transport company, but with freight for different clients), may have its "preferences" depending on the cost of fuel, the wear and tear of the vehicle, the urgency of the delivery, etc. A vote can be used to arbitrate this question.
Still on the topic of autonomous or semi-autonomous vehicles, these generally exchange information between themselves, such as: be careful, there is a danger at such spot on the road, etc. But some vehicles may be riddled with malevolent or malfunctioning software, or just have damaged sensors. In this case, a reputation system can indicate that the information coming from these vehicles is unreliable. This reputation system can be obtained by a vote of the other vehicles.
Intelligent agents voting on behalf of humans
In addition to the above applications, an intelligent agent can also vote to represent a human being.
For example, imagine that you want to organize a meeting with several people. In the future, your personal software assistant may infer your complex preferences on the schedule of this meeting based on your working hours, your personal constraints, other commitments you have and which may be more or less easy to move if needed. It can then consult with the personal assistants of the other participants by a vote.
Similarly, imagine you want a movie suggestion for the whole family, or even for a larger group like attendees at a social event. The personal assistant of each participant can infer their preferences on all the films in the catalog, and then a vote can be performed to suggest a collective choice.
The Plurality rule and the issue of strategic voting
At first glance, the question may seem simple: each voter votes for their preferred option, and the option with the most votes is elected. This voting rule is called Plurality. But imagine the following profile of preferences:
45 voters : A > B > C.
40 voters : B > C > A.
15 voters : C > B > A.
The above notation means, for example, that the first 45 voters prefer option A, then option B, then option C. Using Plurality, option A gathers 45 votes, B has 40 votes and C has 15 votes, so option A wins. But the last 15 voters are extremely dissatisfied: on the one hand, they feel that their ballot did not really weigh in the final decision. On the other hand, they realize that if they had voted strategically for option B, it would have been elected, which may be not ideal for them but still better than option A.
Trying to do better: Instant-Runoff Voting (IRV)
But other voting rules are possible. For example, first eliminate the option with the lowest score, and transfer its votes to the second choice of its voters. Then, the option with the lowest score is again eliminated, and so on. This system has various names depending on the country: Single Transferable Voting (STV), Ranked Choice Voting (RCV), Alternative vote, etc. Here we use its most context-neutral name: Instant Runoff Voting (IRV). This rule is used in various countries: for example, it has been the case in Australia for more than a century.
In our example, what will happen? Option C is eliminated and its votes are transferred to B, who now totals 55 votes, hence B ends up elected. We note, on the one hand, that the ballot of each voter weighed in the final decision. And, on the other hand, it is possible to prove that no voter had an interest in hiding their real preferences by a strategic vote.
So, have we solved the problem already? Unfortunately not, because in some cases, IRV is also sensitive to strategic voting. In our example, just change the preferences of the last 15 voters so that they still prefer C, but now have A as their second choice. Here is the resulting profile of preferences.
45 votes: A > B > C
40 votes: B > C > A
15 votes: C > A > B
Again C is eliminated, but now its votes are transferred to option A, and eventually A wins. However, the 40 voters who prefer B can make a strategic compromise and vote for C: then C will be elected, which is not ideal for them for still better than A.
But where exactly is the problem?
One could think that strategic voting is not really a problem. After all, everyone knows the rules of the game, and even if voting becomes a strategic act, everyone is equal before it. However, this is not entirely true: even if equality remains in principle, there is de facto inequality between, on the one hand, strategic voters who are well informed of the intentions of the others (by guessing them or even by unfair means such as espionage) and, on the other hand, less sophisticated or less well-informed voters.
Moreover, even if human beings are also capable of strategic voting, the problem is even more crucial in the case of software agents, which may have a great computing capacity that they can exploit for establishing complex strategies in contexts using subtle voting rules and/or having a large number of options to choose from.
Good news, bad news
Here is the good news: many other voting rules than Plurality have been studied by scientists for more than two centuries. So, can we hope to find one that is immune to strategic voting?
And this is where the bad news comes in: according to the Gibbard-Satterthwaite theorem (1973), for 3 or more options, the only voting rule immune to strategic voting consists in taking into account only the ballot of one voter, then nicknamed the "dictator". It is easy to verify that this rule is insensitive to strategic voting. Indeed, the dictator has no interest in lying, since their preferences will be directly applied. And the other voters have no interest in strategizing either, since their ballot will simply be ignored. The prowess of the theorem is to show also the converse: this dictatorial rule is actually the only one immune to strategic voting.
However, obviously, this is not really the idea that we have of a democratic voting rule!
Evaluate Voting Rules
Since we cannot completely get rid of strategic voting (except with an obviously unacceptable voting rule), we can at least try to limit its scope by quantitatively evaluating each voting rule. In our latest work, we simulate a large number of elections based on data from the Netflix prize, where users rate films. For each voting rule studied and for each election, we calculate the natural winner, obtained if the voters cast their ballots sincerely. Then we automatically assess whether there exists a group of voters who would benefit from voting strategically. In the end, we thus obtain the proportion of elections where the studied voting rule is sensitive to strategic voting.
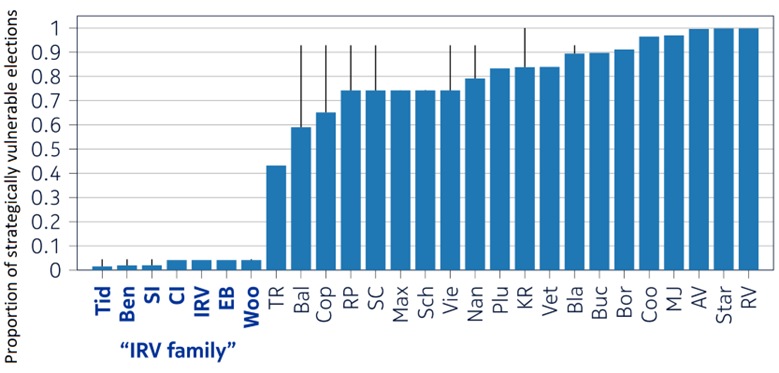
The graph above presents our results. Each label on the x-axis represents a voting rule, e.g. Plurality (Plu), Instant-Runoff Voting (IRV) and many others. The blue bar gives the proportion of elections that are sensitive to strategic voting. The thin black bar represents cases where the problem is too complex algorithmically and where it is unknown whether there exists a strategic opportunity (this can be seen as algorithmic uncertainty).
The results are spectacular: IRV and similar rules, coined the “IRV family”, are vulnerable in less than 5% of elections, far ahead of the next best rule, the Two-Round System (TR), which is vulnerable in more than 40% of elections. For other rules, we can reach vulnerability rates above 80%, like for Plurality, and even close to 100%!
Not all rules are created equal
To summarize, the voting rules are not at all equal when it comes to strategic voting: some are much less vulnerable than others. Our results recommend the use of IRV or a similar rule to aggregate the preferences of intelligent agents, while respecting the fact that each ballot will be used at its fair value.
Reference: François Durand. Coalitional Manipulation of Voting Rules: Simulations on Empirical Data. Accepted for Constitutional Political Economy, 2023. Preprint : [pdf]